Step-by-Step Examples 16-9
4. Show that for every integer n > 0, b
n
× c
n
= a
2n
.
5. Deduce the prime factor decomposition of a
6
.
6. Show that GCD(b
n
,c
n
) = GCD(c
n
,2). Deduce that b
n
and c
n
are prime together.
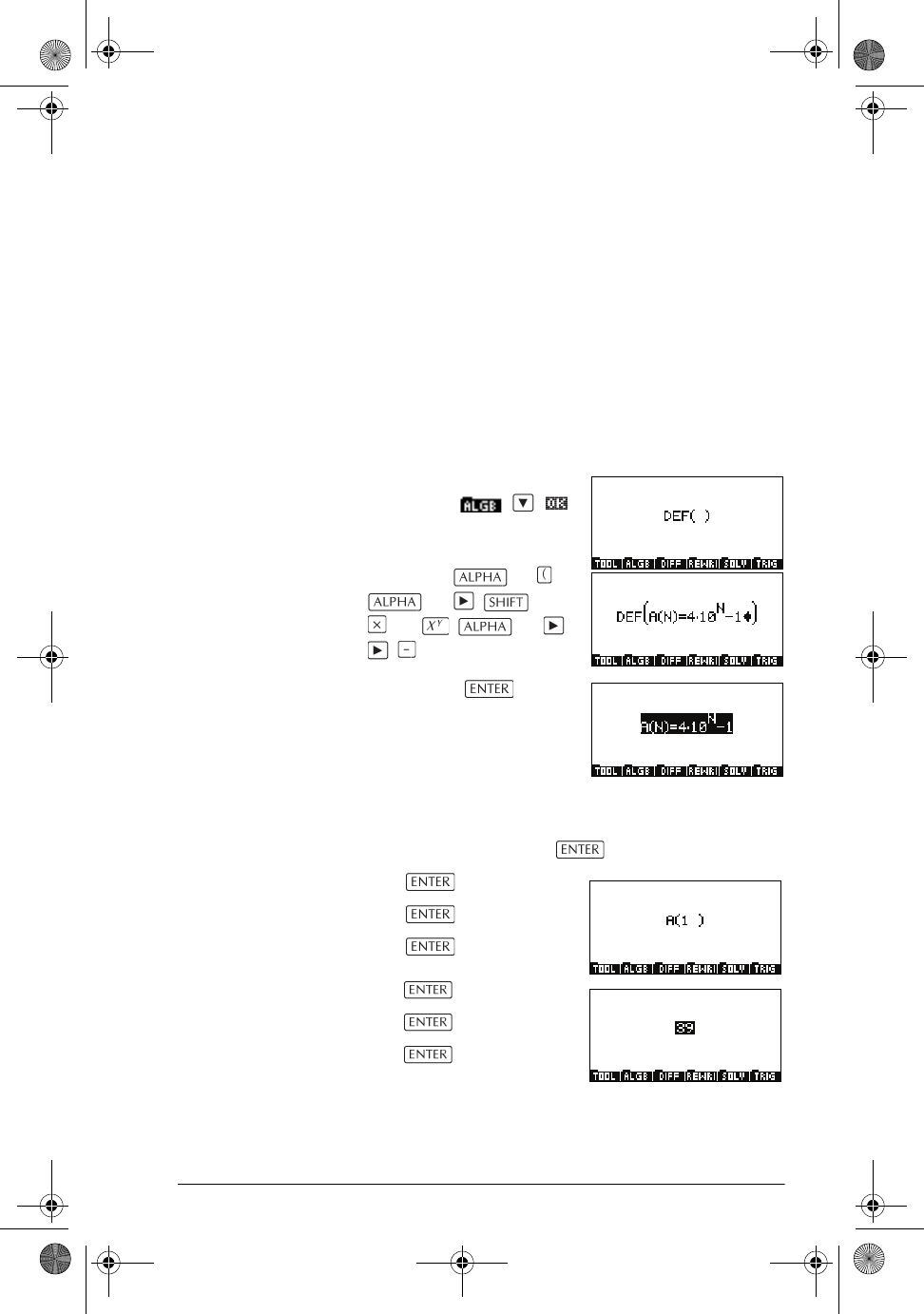
Solution: Begin by entering the three definitions. Type:
DEF(A(N) = 4 · 10
N
–1)
DEF(B(N) = 2 · 10
N
–1)
DEF(C(N) = 2 · 10
N
+1)
Here are the keystrokes for entering the first definition:
First select the DEF command
by pressing .
Now press A
N = 4
10 N
1
Finally press .
Do likewise to define the
other two expressions.
You can now calculate various values of A(N), B(N) and
C(N) simply by typing the defined variable and a value
for N, and then pressing . For example:
A(1) yields 39
A(2) yields 399
A(3) yields 3999
B(1) yields 19
B(2) yields 199
B(3) yields 1999
and so on.
In determining the number of digits the decimal
representations of a
n
and c
n
can have, the calculator is
used only to try out different values of n.
hp40g+.book Page 9 Friday, December 9, 2005 1:03 AM
