6-44
• Graphing is available with Two-Way ANOVA only. V-Window settings are performed
automatically, regardless of Setup screen settings.
• Using the Trace function automatically stores the number of conditions to variable A and the
mean value to variable M, respectively.
k ANOVA (Two-Way)
u Description
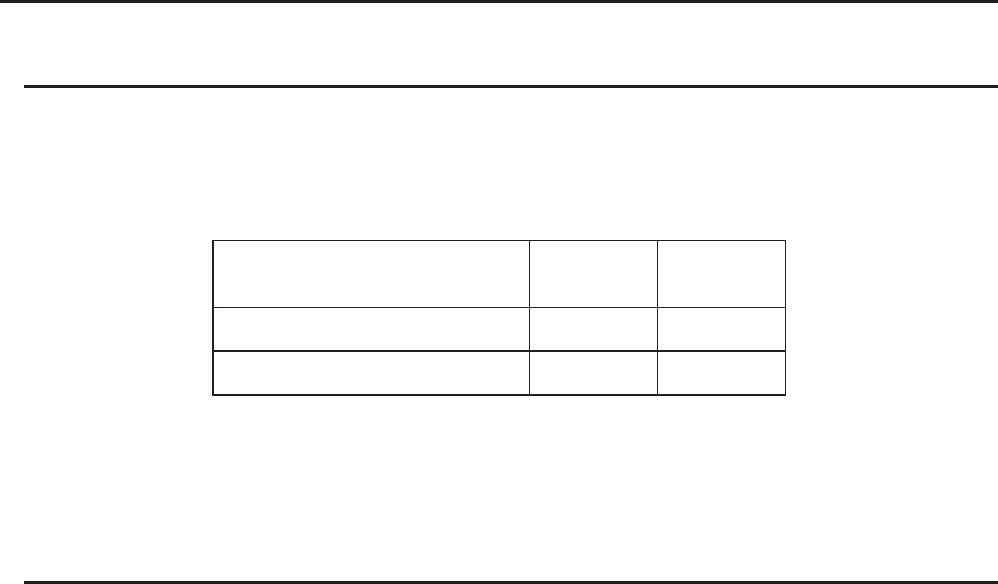
The nearby table shows measurement results for a metal product produced by a heat
treatment process based on two treatment levels: time (A) and temperature (B). The
experiments were repeated twice each under identical conditions.
Perform analysis of variance on the following null hypothesis, using a significance level of 5%.
H
o
: No change in strength due to time
H
o
: No change in strength due to heat treatment temperature
H
o
: No change in strength due to interaction of time and heat treatment temperature
u Solution
Use Two-Way ANOVA to test the above hypothesis.
Input the above data as shown below.
List1={1,1,1,1,2,2,2,2}
List2={1,1,2,2,1,1,2,2}
List3={113,116,139,132,133,131,126,122}
Define List 3 (the data for each group) as Dependent. Define List 1 and List 2 (the factor
numbers for each data item in List 3) as Factor A and Factor B respectively.
Executing the test produces the following results.
• Time differential (A) level of significance P = 0.2458019517
The level of significance (
p = 0.2458019517) is greater than the significance level (0.05), so
the hypothesis is not rejected.
• Temperature differential (B) level of significance P = 0.04222398836
The level of significance (
p = 0.04222398836) is less than the significance level (0.05), so the
hypothesis is rejected.
• Interaction (A × B) level of significance P = 2.78169946e-3
The level of significance (
p = 2.78169946e-3) is less than the significance level (0.05), so the
hypothesis is rejected.
B (Heat Treatment Temperature) B1 B2
A1 113 , 116
133 , 131
139 , 132
126 , 122
A2
A (Time)
B (Heat Treatment Temperature) B1 B2
A1 113 , 116
133 , 131
139 , 132
126 , 122
A2
A (Time)
